Manova

De MANOVA is een analyse techniek om na te gaan of de gemiddelden uitgesplitst over meerdere dimensies van elkaar verschillen.

De ANOVA is een analyse techniek om na te gaan of de gemiddelden van drie of meer groepen van elkaar verschillen. De groepsindeling ligt op één dimensie. Bij een MANOVA is er sprake van meerdere dimensies en dus zijn er ook meerdere (groeps-)gemiddelden te vergelijken. MANOVA staat voor Multivariate ANalysis Of VAriance, of in gewoon Nederlands: meerdimensionele variantieanalyse.

Voortbordurend op het voorbeeld in de ANOVA: stel dat je het vrij besteedbaar inkomen van een gezin wil vergelijken naar het aantal kinderen in het gezin (criterium 1) en naar stedelijk gebied versus landelijk gebied (criterium 2). Je krijgt dan een indeling die vergelijkbaar is met een kruistabel. In de cellen zet je de gegevens: het vrij besteedbaar inkomen van een gezin. Nu is voor ieder cel afzonderlijk, maar ook voor elke cel in de rand het gemiddelde te berekenen. Er is ook een algemeen gemiddelde te berekenen over alle gegevens. Met de MANOVA ga je na of de rand-gemiddelden (van elke dimensie, in dit geval dus twee dimensies of indelingscriteria) statistisch significant afwijken van het algemeen gemiddelde. Dit noemt men een hoofdeffect. Vervolgens ga je na of de cel-gemiddelden van het algemeen gemiddelde afwijken. Dit noemt men het interactie-effect. Tenslotte ga je na hoeveel de individuele waarnemingen dan nog afwijken van het eigen cel-gemiddelde.

De formules in een MANOVA

Dat zijn nogal wat berekeningen. Gelukkig hebben we programmatuur die dit heel snel voor je uit kan rekenen. Het berekenen van de sum of squares gaat op dezelfde manier als bij de ANOVA, alleen het interactie-effect wijkt daar een beetje vanaf. In de tabel hieronder wordt een overzicht gegeven van de te gebruiken formules. In plaats van de j om de groepen aan te duiden, worden nu een k en een r gebruiken als coördinaten voor de kolommen en rijen.

De MANOVA is een analysetechniek om na te gaan of de gemiddelden uitgesplitst over meerdere dimensies van elkaar verschillen.

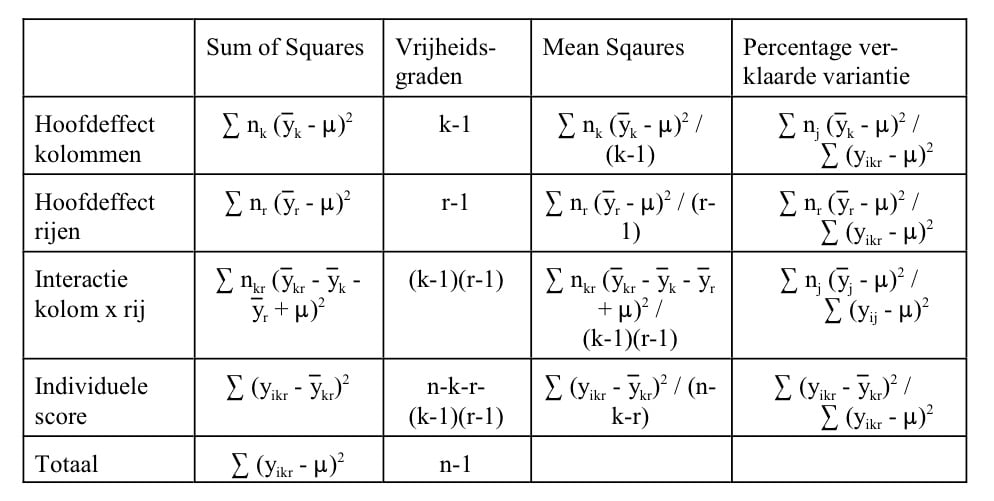
Een illustratie van de MANOVA

In de illustratie hieronder staat een rekenvoorbeeld dat voortborduurt op de gegevens in de ANOVA. We willen er op wijzen dat door het toevoegen van de variabele weliswaar de sum of squares hetzelfde blijft maar er wel andere toetswaarden ontstaan (de F-waarde) en dus ook andere kanswaarden op een significant verband.

De MANOVA is een analyse techniek om na te gaan of de gemiddelden uitgesplitst over meerdere dimensies van elkaar verschillen.
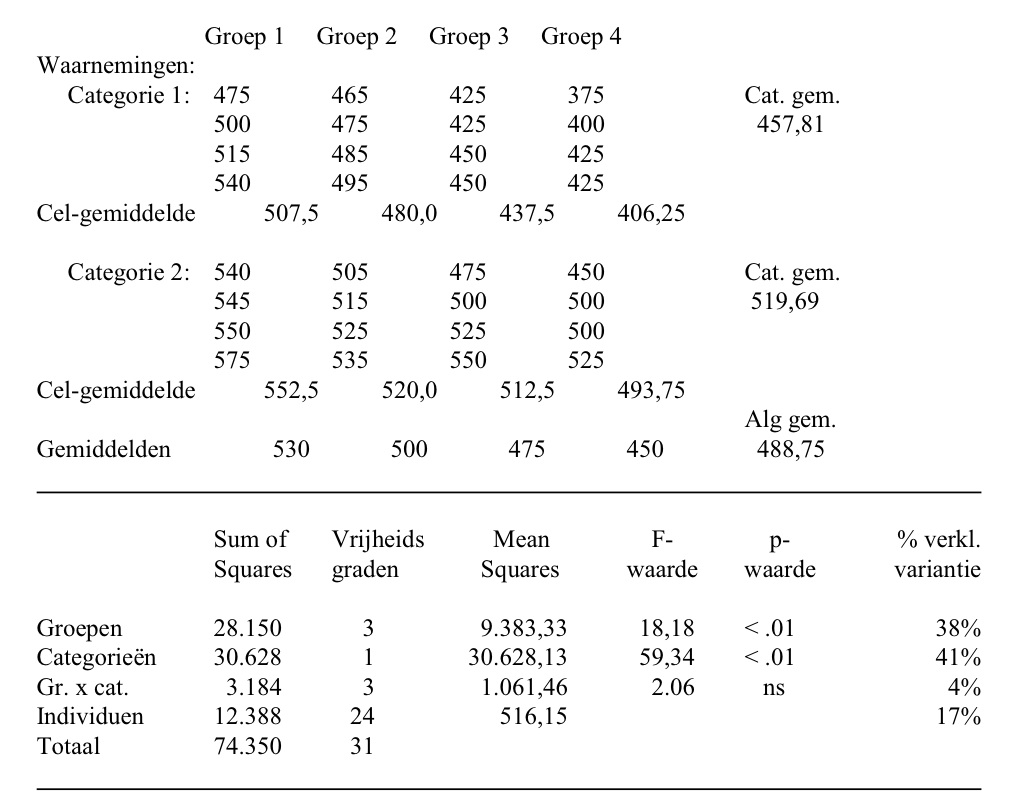
De MANOVA kan voor uiteenlopende situaties worden gebruikt. Er kunnen meerdere onafhankelijke variabelen in het analysemodel worden opgenomen. Deze mogen zelfs 'genest' zijn, dat wil zeggen dat er een onderverdeling binnen een hoofdgroepering is zoals jongens en meisjes in een klas. Het voert te ver om dit hier uit te werken. Het is beter om daar een gespecialiseerd statistiekboek op na te slaan.

Wanneer mag/moet je de MANOVA gebruiken?

Download de handleiding om te bepalen welke statistische toets je mag/moet gebruiken. Daarin word uitgelegd wanneer je welke toets moet gebruiken. In plaats van een MANOVA is het misschien beter om te kiezen voor een ANCOVA of een MANCOVA. Lees het paper en je kunt een onderbouwde beslissing nemen.

De MANOVA in SPSS

Hoewel het wel kan, is het echt niethandig om de berekeningen handmatig uit te voeren. Je kunt veel beter een software programma gebruiken. Hoe dat in SPSS moet leggen we je uit in onze Cursus SPSS.