Hulp bij onderzoek

Om na te gaan of groepen van elkaar verschillen, wordt vaak gekeken naar het gemiddelde. Als de gemiddelden van elkaar verschillen, zegt men dat de groepen van elkaar verschillen. De t-toets gebruik je om de gemiddelden van twee groepen met elkaar te vergelijk. De ANOVA (ANalysis Of VAriance of op zijn Nederlands variantieanalyse) is een toets die wordt gebruikt om na te gaan of er een verschil is tussen de gemiddelden van drie of meer groepen. 

Waarvoor gebruik je de ANOVA?

Voorbeelden van vragen waarvoor je de ANOVA gebruikt zijn:

• Zijn Nederlanders, Belgen en Fransen gemiddeld genomen even lang?
• Is de aardappeloogst rijker op zandgrond, kleigrond of veengrond?
• Is de tevredenheid over de zorg beter in gemeente A, B of C?

Niet alleen is het belangrijk dat er 3 of meer groepen worden onderscheiden, maar ook dat de afhankelijke variabele een continue verdeling heeft. Dat zal bij de eerste twee van de hierboven gegeven voorbeeld-vragen zeer waarschijnlijk wel het geval zijn, maar bij de derde is het twijfelachtig. Als je tevredenheid hebt gemeten op een 5-punts Likertschaal niet - in dat geval zou je de Mann-Whitney toets moeten gebruiken - maar als het een samengestelde variabele is vermoedelijk weer wel. Daarom is het erg belangrijk om te weten met wat voor variabelen je te maken hebt. Dat is ook bepalend voor welke toets je mag gebruiken. Je leest hier meer over in het paper Welke toets mag/moet je gebruiken.

Tot zover het verhaal over de ANOVA zonder ons druk te maken om de rekentechniek. Hieronder leggen we wat meer uit over de rekentechnische aspecten. Niet dat je dat nou helemaal moet doorgronden, maar het is wel handig om daar iets van te weten zodat je de uitkomsten uit de analyses beter kunt interpreteren.

Het 'rekenwerk' in een ANOVA

Het principe van de ANOVA als toets is relatief eenvoudig.

Stel je hebt drie groepen: Nederlanders (N), Belgen (B) en Fransen (F). Stel, je hebt in elke groep 100 personen en van die personen heb je de lengte gemeten. Een individueel persoon duiden we aan met: y_(i). Als het gaat om een Nederlander dan duiden we dat aan met y_(iN), een Belg met y_(iB) en een Fransman met y_(iF).

Uit de gemeten waarden bereken je een algemeen gemiddelde; dit wordt aangeduid met de Griekse letter µ. In dit geval is dat dus de gemiddelde lengte van alle 300 personen.

Ook voor iedere groep is een gemiddelde te berekenen. Dit wordt aangeduid met y_(j) (daar moet een streepje boven maar dat wil niet met deze editor). Je hebt dus een gemiddelde voor de lengte van de Nederlanders (y_N), de Belgen (y_B) en de Fransen (y_F).

Er kunnen nu drie soorten varianties worden berekend:
1) de variantie als gevolg van de afwijking van de groepsgemiddelden ten opzichte van het algemene gemiddelde (y_(j) t.o.v. µ). Dit is de variantie tussen de groepen.
2) de variantie van elke onderzoekeenheid ten opzichte van het groepsgemiddelde (alle individuen in een groep t.o.v. het groepsgemiddelde. Dus y_(iN) t.o.v. y_(N), y_(iB) t.o.v. y_(B) en y_(iF) t.o.v. y_(F)). Dit is de variantie binnen de groepen.
3) de variantie van elke onderzoekseenheid ten opzichte van het algemeen gemiddelde (alle individuen t.o.v. het algemeen gemiddelde. Dus y_(i) t.o.v. µ). Dit is de totale variantie.

De totale variantie (3) bestaat dus uit de variantie tussen de groepen (1) + de variantie van de individuen t.o.v. het groepsgemiddelde (2). Je kan nu vaststellen hoeveel procent van de groepsvariantie deel uitmaakt van de totale variantie (= 1/3) en hoeveel procent van de individuele variantie binnen de groepen deel uitmaakt van de totale variantie (= 2/3). Op die manier kun je aangeven hoeveel procent van de totale variantie verklaard kan worden door die groepsindeling. Alles wat niet door die groepsindeling verklaard kan worden noemt men dan de niet verklaarde variantie, of de restvariantie of de error.

Met een ANOVA wil je nagaan of de variantie tussen de groepen substantieel is. Dat wil zeggen, is de variantie tussen de groepen voldoende groot om te kunnen zeggen dat de drie gemiddelden van elkaar verschillen. Immers, als de variantie tussen de groepen 0 is, dan is er ook geen verschil tussen de gemiddelden. Het moet dus wel iets meer zijn, maar wanneer is het substantieel meer? Wanneer is het statistisch significant?

Om dat vast te stellen ga je de variantie van de groepsgemiddelden delen door de variantie van de individuele onderzoekseenheden t.o.v. de groepsgemiddelden (dat is dus het delen van twee varianties, vandaar variantieanalyse). Maar deze vergelijking is niet helemaal eerlijk, want de verschillen tussen de groepen is gebaseerd op een klein aantal groepen terwijl die binnen de groepen gebaseerd is op heel veel individuen. Daarom deel je eerst de varianties door het aantal vrijheidsgraden. Je berekent dan een F-waarde en die is te vergelijken met een F-waarde in een tabellenboek. En als de berekende F-waarde groter is dan de kritieke waarde in de tabel, dan zegt men dat er een statistisch significant verschil is (zie het toetstheorema van Fisher).

Er is nog een beperkende factor: varianties mag je niet bij elkaar optellen of delen. Daarom gebruikt men slechts een deel van de formule: alleen het deel dat boven de deelstreep staat voor het berekenen van de variantie (zie voor de formule bij het begrip standaarddeviatie). Het deel dat boven de deelstreep staat wordt de sum of squares (afgekort tot SoS) genoemd. Als je de sum of squares deelt door het aantal vrijheidsgraden, krijg je de mean squares (afgekort als MS). Een overzicht van de te gebruiken formules staat in het schema hierna: 

Het berekenen van de toetswaarde (de F) is het delen van de mean square van de groepsscore door de mean square van de individuele score (zie de formule hieronder). Dit is een beetje tegen de verwachting in; zonder nadenken zou je kiezen voor het totaal. Er wordt echter getoetst als de eigen variantie gedeeld door het restant van de totale variantie (oftewel het totaal minus de eigen variantie).

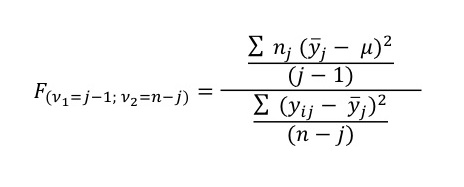
Een voorbeeld van een ANOVA

In onderstaande illustratie staat een rekenvoorbeeld met een beperkte aantal waarnemingen.

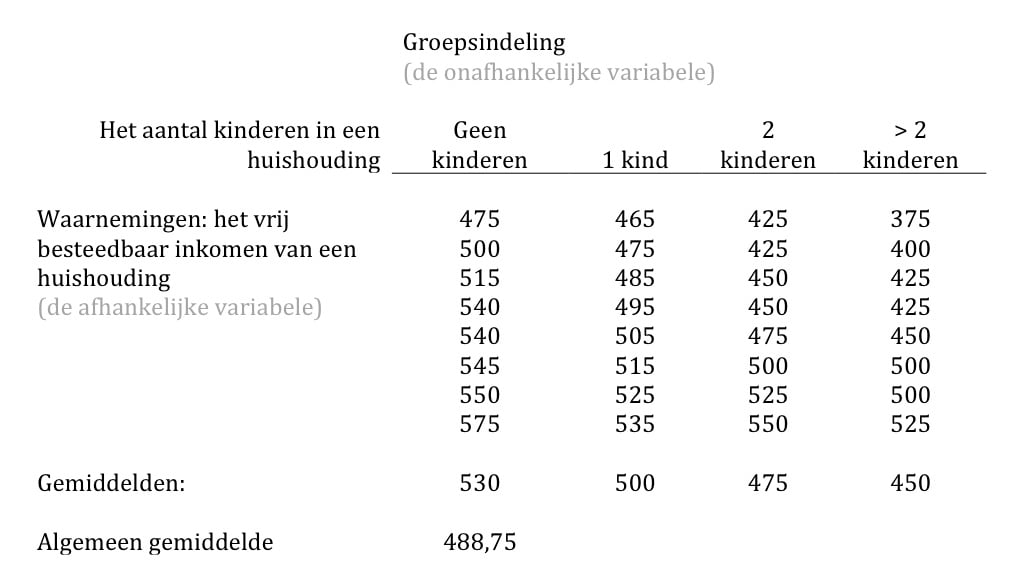
Op basis van deze gegevens zijn de SoS te berekenen. Gebruik daarvoor de formules zoals die in de tabel hiervoor zijn gegeven. Het zijn altijd dit soort tabellen die je in een statistische analyse ziet en die je moet interpreteren.

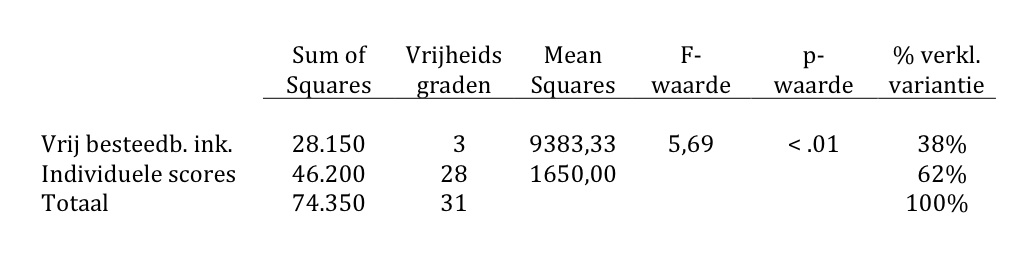
De berekende F-waarde wordt vergeleken met een F-waarde in de tabel. De berekende F-waarde is groter dan de F-waarde in de tabel en daarom is er een statistisch significant resultaat. Ook kunnen we de percentages tussen de SoS vaststellen. En dat is dan het percentage verklaarde variantie. Uit deze analyse mag je alleen concluderen dat de vier groepsgemiddelden statistisch significant van elkaar verschillen. Waar dat nou precies in zit, is nog niet duidelijk. Tussen groep 1 en 4 zit het grootste verschil, dus dat zou de oorzaak voor het significante resultaat kunnen zijn, maar misschien is er ook nog een statistisch significant verschil tussen groep 1 en 3, of tussen 1 en 2. Dit moet je door middel van aanvullende analyses (t-toetsen) trachten te achterhalen.

© Foeke van der Zee (versie 2023). hulpbijonderzoek.nl/online-woordenboek

- specialist in Onderzoek en Statistiek
- auteur van boeken over onderzoeksmethodologie
- oprichter van en coach bij Hulp bij Onderzoek

Een ANOVA in SPSS uitvoeren is eigenlijk supermakkelijk. Je kunt het zelfs op drie manieren doen! En er zijn veel extra's mogelijk! Bekijk onze video daarover in de Online Academie.

Aan ANOVA gerelateerde onderwerpen:

- MANOVA
- t-toets voor groepen
- Kruskal-Wallis toets

Terug naar de begrippenlijst

Word lid van Hulp bij Onderzoek en krijg dit document gratis + gratis proeflessen over methodologie, statistiek en SPSS.