Chikwadraattoets voor kruistabellen en frequenties

De chikwadraattoets wordt wel vaker gebruik, maar er zijn twee situaties waarin hij juist heel expliciet wordt gebruikt, namelijk: 1) bij een frequentieverdeling; 2) bij een kruistabel.

De formule voor de chikwadraattoets

In beide gevallen gaat het om het vaststellen van een verschil tussen de frequenties van voorkomen in een geobserveerde en een verwachte verdeling. De formule die je moet gebruiken is in deze beide gevallen ook hetzelfde: Formule van de chikwadraattoets

De chikwadraattoets bij een frequentieverdeling

In deze situatie heb je een rij met getallen genoteerd, bijvoorbeeld of mensen tevreden zijn over hun woning. Deze reeks getallen wil je vergelijken met een verwachte rij getallen. Nu rijst er een probleem, want hoe stel je de verwachte reeks op? In dit concrete geval zou je een evenwichtige verdeling van 20% per cel kunnen nemen, maar je mag ook een andere verdeling poneren. In het voorbeeld hieronder hebben het laatste gedaan. Vervolgens vul je de formule in en trek je de conclusie. Bijvoorbeeld: 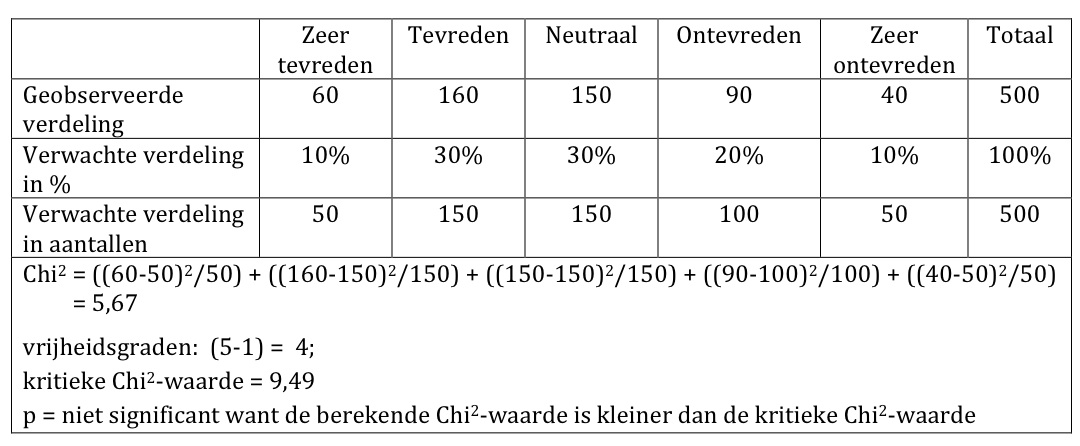Voorbeeld van een chikwadraattoets voor een reeks Het aantal vrijheidsgraden komt overeen met het aantal cellen minus 1.

De chikwadraattoets voor een kruistabel

Bij een kruistabel worden de waarden van twee kenmerken (gemeten op nominaal niveau) tegen elkaar uitgezet: op de kolommen-as komen de waarden van de scores op het ene kenmerk en op de rijen-as komen de waarde van de scores op het andere kenmerk. Op deze wijze krijg je een kruistabel. Per cel wordt de frequentie van voorkomen van iedere combinaties genoteerd. De verwachte waarde is het product van de randtotalen gedeeld door het algemene totaal. Het berekenen van de chikwadraatwaarde is nu vrij simpel. Hieronder vind je een aantal voorbeelduitkomsten. 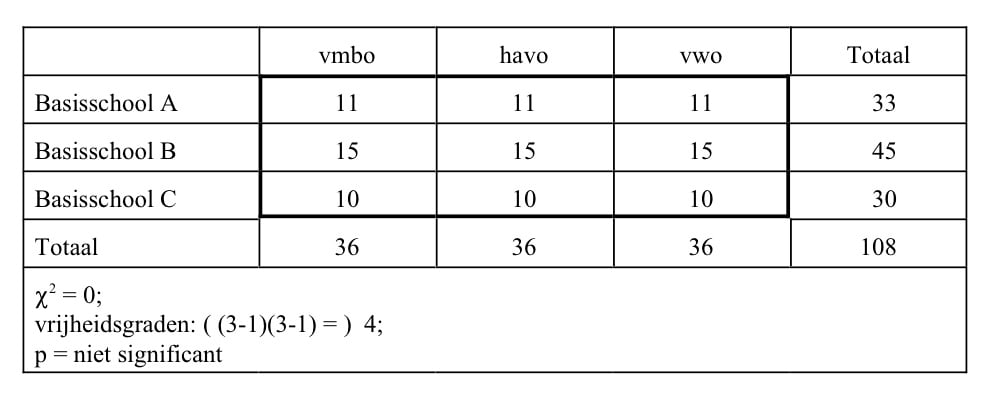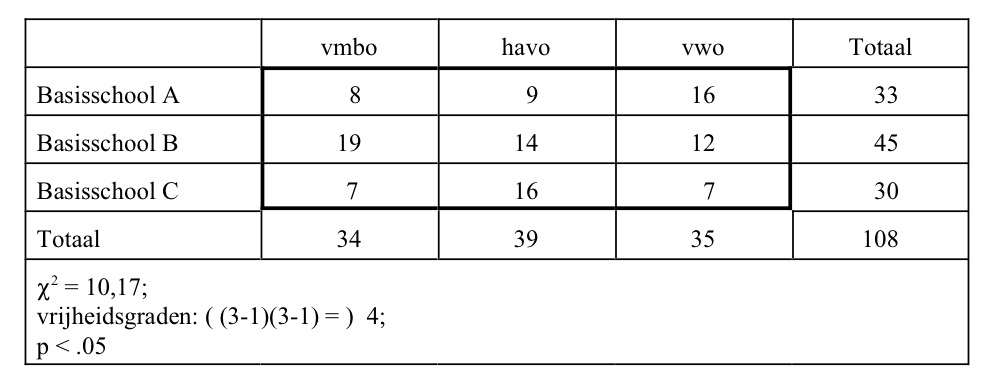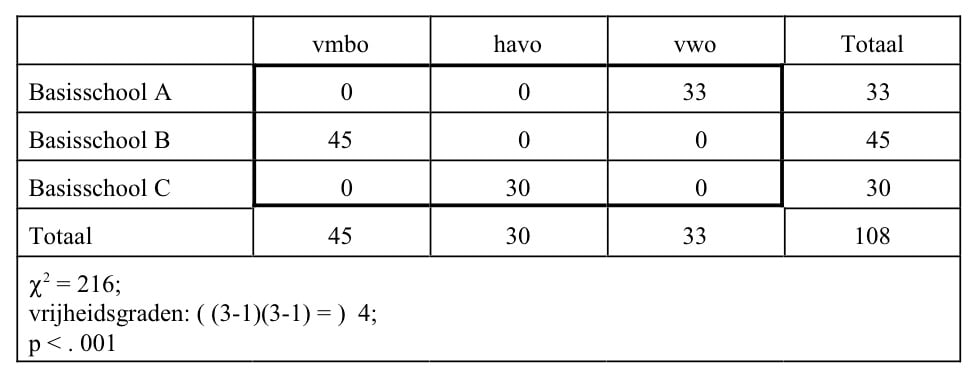Erste voorbeeld van een chikwadraattoets voor een kruistabel Tweede voorbeeld van een chikwadraattoets voor een kruistabel Derde voorbeeld van een chikwadraattoets voor een kruistabel In bovenstaande illustraties zijn de toetsresultaten in de onderste rij van de tabellen geplaatst. In de eerste tabel valt het op dat als er een precies evenwichtige verdeling is, de Chi2-waarde 0 is. In de laatste tabel is de Chi2-waarde 216. Dit is tevens de maximum-waarde, maar dat is alleen in dit geval zo. Indien je andere aantallen hebt, verandert de maximale Chi2-waarde. In principe loopt de Chi2-waarde van 0 tot plus oneindig. Daardoor is de uitkomst van deze berekening moeilijk te interpreteren en wordt er daarom vooral gelet op de p-waarde. De p-waarde geeft aan of de analyse een significant verschil oplevert, en zo ja hoe sterk.