Hulp bij onderzoek

Regressieanalyse is een statistische analysetechniek om de variantie in een variabele te verklaren uit andere variabelen.

De basis van regressieanalyse is correlatierekening

Als je twee variabelen tegen elkaar uitzet, levert dat een puntenwolk op. Hieronder staan drie voorbeelden: 

De samenhang in zo'n puntenwolk kun je beoordelen door de productmoment correlatie uit te rekenen. In de productmoment correlatie betekent de uitkomst 0 dat er helemaal geen samenhang is en de uitkomst 1 (of -1) dat er een perfecte samenhang is. De perfecte samenhang geeft aan dat er een één op één relatie is, oftewel een volstrekt rechte lijn. Dat is mooi, want als je de score op het ene kenmerk weet, dan weet je de score op het andere kenmerk ook. Bij een correlatie die niet gelijk is aan 1 ligt dat verband wat losser, maar ook hier geldt (bij een positieve relatie): als de waarde op de ene variabele stijgt dan stijgt de waarde op de andere variabele ook. Je kunt er dus wel iets over zeggen, maar je moet wat slagen om de arm houden.

Stel nu eens dat er een relatie is tussen de lengte van de partners in een huwelijk: lange mensen trouwen met elkaar en korte mensen trouwen met elkaar. Op zich niet eens een rare veronderstelling. Als je nu weet hoe lang de ene persoon is, dan zou je ook iets kunnen zeggen over de lengte van zijn partner. Toch? Maar hoe bereken je dat dan?

De regressielijn

In de algebra heeft een rechte lijn de formule van y = a + bx, waarbij de a en de b constanten zijn die de kenmerken van de rechte lijn bepalen. De a geeft aan waar de lijn de y-as passeert (het intercept) en de b geeft aan hoe schuin die lijn loopt (de regressiecoëfficiënt). Op de middelbare school werd de functie gegeven (bijvoorbeeld: y = 2 + 3x) of leerde men die functie te berekenen uit twee punten (bijvoorbeeld uit de punten (0, 1) en (1, 3)).

In de statistiek gebeurt hetzelfde: je moet de lijn berekenen op grond van de gegeven waarden op de variabelen. Er is echter één groot verschil: je neemt niet willekeurig twee punten, maar je gebruikt alle punten die gevormd worden door de waarden op de beide variabelen. In de illustratie hieronder staan dezelfde puntenwolken als bij de productmoment correlatie. Door die puntenwolk is een rechte lijn getrokken. Dat is de te vinden regressielijn. 

Het berekenen van de regressiecoëfficiënten

En hoe bereken je nou die regressielijn uit al die punten? De formule voor het berekenen van de b is de volgende: 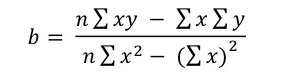 In deze formule valt het op dat er veel overeenkomstige berekeningen moeten worden gemaakt als in de productmoment correlatie. Die b en de pm-correlatie zijn inderdaad heel direct aan elkaar gerelateerd. De b zou je ook uit de pm-correlatie kunnen berekenen. De formule daarvoor is de volgende (waarbij het opvalt dat de b bepaald wordt door de standaarddeviaties van en de correlatie tussen de twee variabelen):  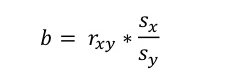En nu je de waarde van b weet kan je ook relatief eenvoudig de waarde van a vinden: 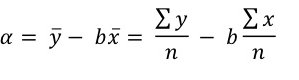De formule voor de lijn die nu ontstaat, is de beste rechte lijn: de afwijking van alle punten die in ogenschouw zijn genomen ten opzichte van deze lijn is het kleinst. Elke willekeurige andere lijn zal een grotere afwijking laten zien. Daarom noemt men dit de ordinary least square (OLS-) regressie. Ordinary is Engels en het betekent niet ordinaire maar gewone. Het is dus de gewone kleinste kwadraten methode voor regressieanalyse.

Twee illustraties van regressieanalyse

Stel je moet een voorspelling maken over de lengte van een vrouw op basis van de lengte van de man. Uit onderzoek blijkt dat er een regressielijn geldt van y = -0,10 + 1,02x, waarbij de y staat voor de lengte van de vrouw en de x voor de lengte van de partner. Als je weet dat de lengte van de partner 1,98 meter is, wat schat je dan als lengte van de vrouw? Je kunt daarvoor het beste de gegevens in de formule invullen. De uitkomst is 1,91 meter. En als de partner een lengte heeft van 1,65? Dan zal de vrouw vermoedelijk een lengte hebben van 1,58. Het zal in de praktijk nooit helemaal kloppen, maar de voorspelling is wel beter dan wanneer je helemaal niets zou weten.

Is dit nou handig om te weten? Het bovenstaande voorbeeld was met opzet nogal simpel om het principe van regressieanalyse duidelijk te maken. Daarom ook nog een ander voorbeeld. Als je weet dat met het ouder worden de zorgkosten omhoog gaan, dan zou je een voorspelling kunnen maken hoe hoog de kosten over een bepaalde tijd zullen zijn. De zorgkosten zijn per individu te bepalen en gesommeerd over de individuen voor een hele samenleving. Zeer waarschijnlijk is niet alleen de leeftijd van de persoon van invloed op de zorgkosten, maar spelen ook technische ontwikkelingen, persoonlijke omstandigheden en nog veel meer aspecten een rol. Zodra je meerdere aspecten in je analyse betrekt, doe je niet meer een univariate regressieanalyse maar een multivariate regressieanalyse. De gangbare term voor multivariate regressieanalyse is multipele regressieanalyse.

© Foeke van der Zee (versie 2023). hulpbijonderzoek.nl/online-woordenboek

- specialist in Onderzoek en Statistiek
- auteur van boeken over onderzoeksmethodologie
- oprichter van en coach bij Hulp bij Onderzoek

Aan regressieanalyse gerelateerde trefwoorden:

- Productmoment correlatie
- strong>Multipele regressie
- Multipele correlatie

Terug naar de begrippenlijst