Multipele correlatie

Multipele correlatie is de samenhang tussen meerdere variabelen op interval/ratio niveau. Dit wordt aangeduid met een hoofdletter r: R. Maar veel liever letten we nog op het kwadraat: de R². Dat is het percentage verklaarde variantie. Laten we dat eens uitleggen.

Correlatie en multipele correlatie

De meest bekende maat voor samenhang is de Pearson productmoment correlatie (afgekort tot pm-correlatie). De pm-correlatiecoëfficiënt geeft de kracht van de samenhang aan. Deze ligt tussen de -1 en de 1. Bij de waarde van -1 en +1 is er sprake van een perfecte samenhang: de gegevens liggen op één rechte lijn; een waarde op de x-as komt overeen met één waarde op de y-as. Bij een waarde van 0 is er helemaal geen samenhang. Door de pm-correlatiecoëfficiënt te kwadrateren en te vermenigvuldigen met 100%, krijg je het percentage verklaarde variantie. Dat percentage ligt dus altijd tussen de 0 en 100%. Als r = 0 dan wordt er 0% van de variantie van Y door X verklaard, en bij de waarde 1 is dat 100%. Dat percentage verklaarde variantie zou je ook de gemeenschappelijke variantie kunnen noemen. Dat kun je ook uitbeelden in venndiagrammen.

Venndiagrammen van correlatie

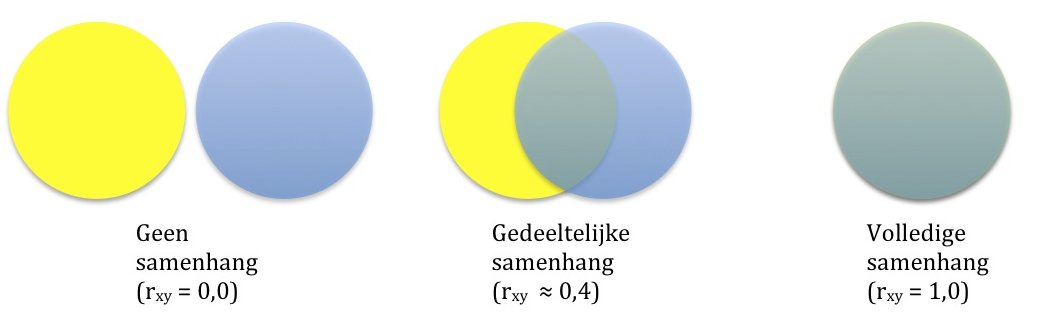
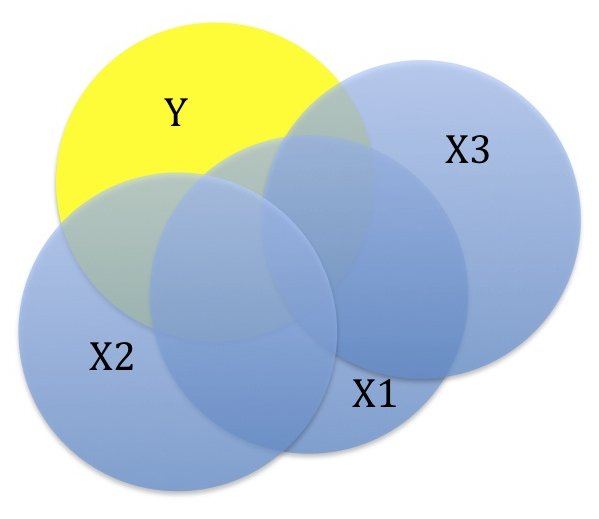
Bij multipele correlatie wil men niet de samenhang tussen twee variabelen weten, maar tussen meerdere variabelen. Je kunt je dat voorstellen door niet twee cirkels (de X en de Y) over elkaar heen te leggen, maar meerdere cirkels op de Y-cirkel te leggen. Door steeds maar meer cirkels toe te voegen kan er steeds een stukje verklaarde variantie erbij komen. Dat wordt hieronder uitgebeeld met 3 X-variabelen en 1 Y-variabele.

Venndiagam van multipele correlatie

Interpreteren van de multipele correlatiecoëfficiënt

De kracht van de samenhang (de correlatiecoëfficiënt) wordt als er sprake is van meerdere variabelen niet meer aangeduid met de letter r, maar met de hoofdletter R. De R kan alleen waarden aannemen die liggen tussen 0 en 1. Bovendien is het vaak beter om te spreken in termen van het percentage verklaarde variantie en dat wordt aangeduid met R². Het kan zijn dat als er nog een variabele wordt toegevoegd dat er dan niks nieuws meer van Y wordt afgedekt. De nieuwe variabele voegt dan niets meer toe. In bovenstaand venndiagram zou de nieuwe variabele in het blauwe gebied komen te liggen.

De adjusted multipele correlatiecoëfficiënt

Statistici onderscheiden ook de adjusted R². Dat is een correctie op de gewone R²: er wordt een correctie gemaakt op basis van het aantal variabelen en het aantal cases of respondenten. De adjusted R² kan zelfs negatief zijn (en dat is opmerkelijk voor een kwadraat). Dat treedt vooral op bij een lage samenhang en/of een kleine n. Als de R² en de adjusted R² niet veel van elkaar verschillen, zit het wel snor.

Multipele correlatie en regressieanalyse

De multipele correlatiecoëfficiënt is een belangrijk onderdeel van regressieanalyse. Hiermee ben je in staat verschillende modellen met elkaar te vergelijken. Dat is erg belangrijk om na te gaan of er sprake is van mediatie, moderatie of bij hiërarchische regressieanalyse. We vertellen je daar veel meer over in de Cursus Statistiek. Als je wilt weten hoe je dat uitvoert in SPSS, bekijk dan onze video's uit de reeks Cursus SPSS.