Steekproefgrootte

De steekproefgrootte is van belang als je een statistisch verschil wil aantonen. Bij een te kleine steekproef zijn er geen verschillen te vinden, bij een te grote is alles statistisch significant verschillend. Je moet een optimum vinden.

Waarom moet je vooraf de steekproefgrootte vaststellen?

Het is van groot belang om van te voren vast te stellen hoe groot de steekproef moet zijn om de statistisch significante verbanden en verschillen op hun relevantie te kunnen beoordelen. Als de onderzoeker bij te veel onderzoekseenheden gegevens gaat verzamelen dan maakt hij te veel kosten en zijn mogelijk alle statistische analyses significant. Worden daarentegen bij te weinig eenheden gegevens verzameld, dan geeft mogelijk geen enkele statistische analyse een significante uitkomst en/of zijn de conclusies niet stabiel. Alle reden dus om vooraf de steekproefgrootte vast te stellen. Maar wat is dan optimaal?

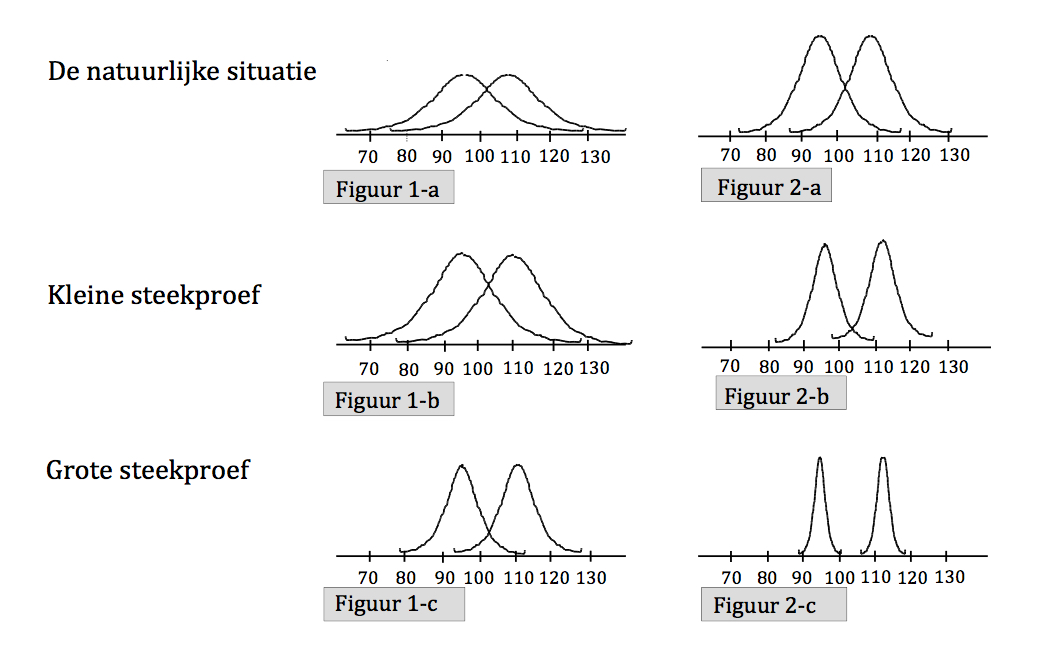
Stel dat je een kenmerk wilt onderzoeken met een vrij vlakke verdeling. Het verschil tussen de gemiddelden van twee groepen kun je uitbeelden zoals in figuur 1-a van de illustratie. De veronderstelde gemiddelden van beide groepen liggen relatief dicht bij elkaar en door de grote spreiding waarbinnen de gemiddelden kunnen liggen, zijn ze ook nauwelijks van elkaar te onderscheiden. Je kan de spreiding in het verschil tussen rond het gemiddelde vernauwen met een factor van sd/wortel(n).

Neem je nu een te kleine steekproef, dan ontstaat een situatie zoals in figuur 1-b: het verschil in gemiddelden is weliswaar groter geworden, maar is nog steeds niet erg groot. Een onderzoek waarin een verschil zou moeten worden aangetoond, had net zo goed niet plaats hoeven vinden omdat niet te verwachten is dat er statistisch significante resultaten uit komen.

Vergroot je de steekproef, dan ontstaat een situatie als in figuur 1-c. Daarvan is wel te zeggen dat er mogelijk statistisch significante resultaten uit de analyses kunnen komen.

Heeft het kenmerk echter een verdeling zoals in figuur 2-a van de illustratie is uitgebeeld, dan kan je met een kleine steekproef volstaan. Uit figuur 2-b blijkt dat er voldoende onderscheidend vermogen is. Ga je in deze situatie toch door met het verzamelen van data bij meer onderzoekseenheden, dan krijg je een situatie zoals in figuur 2-c: in de statistische analyses zal je een enorm statistisch significant verschil aantonen. Je hebt nu veel te veel energie en financiële middelen verspeeld. Daarom is het wenselijk om situaties zoals die in afbeelding 1-c of 2-b zijn geschetst te hebben.

Aannames voor het berekenen van de steekproefgrootte

Voor het vaststellen van de grootte van de steekproef zal je dus min of meer de natuurlijke situatie moeten weten. Maar die is niet altijd bekend. In dat geval zal je aannames moeten maken. De bestaande statistische boeken bespreken alleen hoe je de steekproefomvang kunt bepalen voor een normaal verdeling of voor een proportie. Ik heb een methode ontwikkeld waarmee je ook de minimale steekproefomvang kunt berekenen voor t-toetsen, frequentie verdelingen en kruistabellen.

Veel studieboeken beschrijven één manier om de steekproefomvang te bepalen. Deze is alleen bruikbaar voor het schatten van een proportie (in de populatie). Daar komt altijd 384,2 (afgerond 385) uit. Aan deze manier om de steekproef te bepalen heb je helemaal niets, want in 99,9% van de onderzoeken moet er helemaal geen proportie van de populatie worden geschat.

Hoe je het wel aan moet pakken leg ik uit in het paper bepalen van de steekproefgrootte. Ik raad je aan om dat te downloaden. Dan weet je hoe je het moet aanpakken.