Wilcoxon-toets

De Wilcoxon-toets wordt gebruikt voor het vaststellen van een verschil tussen twee kenmerken op ordinaal niveau bij dezelfde onderzoekseenheid.

Wanneer gebruik je de Wilcoxon-toets?

Bijvoorbeeld, in een schaatswedstrijd krijgt iedere deelnemer een eindscore (1e, 2e, 3e, etc.). In het jaar daarop doen precies dezelfde deelnemers weer mee en wordt opnieuw de rangordescore vastgesteld. De vraag is nu of er verschillen zijn opgetreden: is degene die vorig jaar eerste was nu ook weer eerste, en is de tweede van vorig jaar nu ook weer tweede etc.? Er is sprake van geen verschil als de schaatser in het eerste jaar precies dezelfde positie inneemt als in het voorgaande jaar. Dat zal nooit helemaal het geval zijn. Hoe stel je vast of er verschillen zijn?

Het rekenwerk van de Wilcoxon-toets

Om na te gaan of er veel verschil is (het ‘stuivertje verwisselen’) bereken je het verschil in plaats tussen het eerste en het tweede jaar. Van eerste naar tweede plaats is dus -1; en van tweede naar eerste plaats is +1; en van derde naar vierde plaats is ook -1; en van zesde naar derde plaats is +3. Vervolgens rangorden je deze verschilscores. Bij ex aequo verdeel je de rangorde-score. Tenslotte tel je de rangorde-scores bij elkaar op bij alleen die uitkomsten waar deze een negatieve waarde hebben. Dit is de W-waarde. Deze W-waarde wordt getoetst met de volgende formule.

Formule Wilcoxon-toets

Een rekenvoorbeeld van de Wilcoxon-toets

Lastig uit te leggen, maar een voorbeeld met getallen maakt het meteen veel duidelijker:

Rekenvoorbeeld van een Wilcoxon-toets

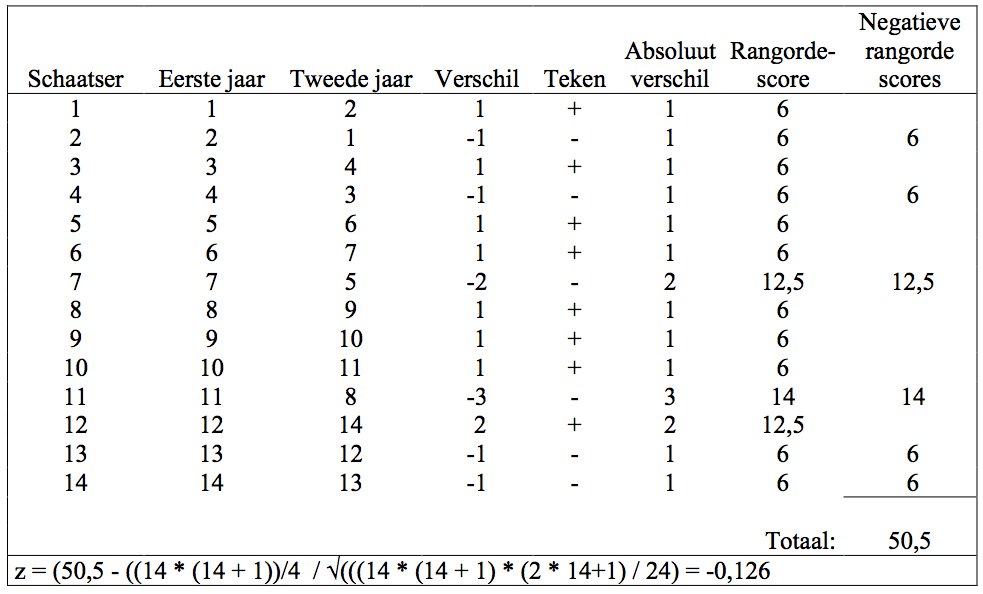
De berekende z-waarde toont aan dat er geen statistisch significant verschil bestaat tussen de volgorden van beide jaren.

De Wilcoxon-toets en Likertschalen

Het voorbeeld van de Wilcoxon-toets hierboven is er eentje zoals je die in menig statistiekboek tegenkomt. Iedere schaatser is al gerangordend van 1 (de snelste) tot 14 (de langzaamste). Het gaat om een ordening in respondenten of cases.

In doorsnee onderzoek gebruiken we de Wilcoxon-toets meer voor iets als het vergelijken van het kerstrapport en zomerrapport, of voor de tevredenheid over de keuken en de tevredenheid over de slaapkamer. Deze scores zijn nog helemaal niet geordend tussen personen. Je kunt de Wilcoxon-toets nog steeds gebruiken. Het gaat immers over het verschil tussen beide metingen. De tevredenheid over de slaakamer (bijvoorbeeld een 4) en de tevredenheid over de keuken (ook een 4) is een verschil van 0. Deze verschilscores worden gerangordend en krijgen een score. De rest van de berekening gaat dan weer hetzelfde.

Handmatig berekenen van de Wilcoxon-toets?

Het met de hand berekenen van de Wilcoxon-toets is op zich niet zo moeilijk, maar het vergt wel enige tijd en je maakt makkelik rekenfouten. Het is beter om dat door een software programma te laten doen. Hoe dat moet in SPSS . In onze Cursus SPSS leren we je hoe je een Wilcoxon-toets in SPSS uitvoert.