Hulp bij onderzoek

Cramers V is een maat voor een samenhang tussen variabelen op nominaal niveau. De kruistabel hoeft niet vierkant te zijn; Cramèrs V kan ook uitgerekend worden voor rechthoekige tabellen.

Hoe wordt Cramers V berekend?

Cramèrs V wordt berekend met behulp van deze formule:  De uitkomst ligt altijd tussen 0 en 1. Een waarde van 0 betekent dat er geen samenhang is: de waarden van de ene variabele liggen evenredig verspreid over de waarden van de andere variabele. De waarde van 1 betekent dat er een perfecte samenhang is: voor elke waarde van de ene variabele geldt dat deze precies overeenkomt met één waarde van de andere variabele. Omdat het gaat om variabelen op nominaal niveau is de volgorde van de waarden niet belangrijk: men mag deze zondermeer van plaats verwisselen. Als er een perfecte samenhang is, kunnen de waarden zodanig verplaatst worden dat alleen de cellen op de diagonaal gevuld zijn en de rest leeg. Het maakt dan ook niet uit of dit de diagonaal van linksboven naar rechtsonder is, of van linksonder naar rechtsboven. Het teken zoals men dat bij de productmoment correlatie, de Spearman rangcorrelatie of bij Kendall's tau tegenkomt, is niet van belang.

Voorbeelden van Cramers V

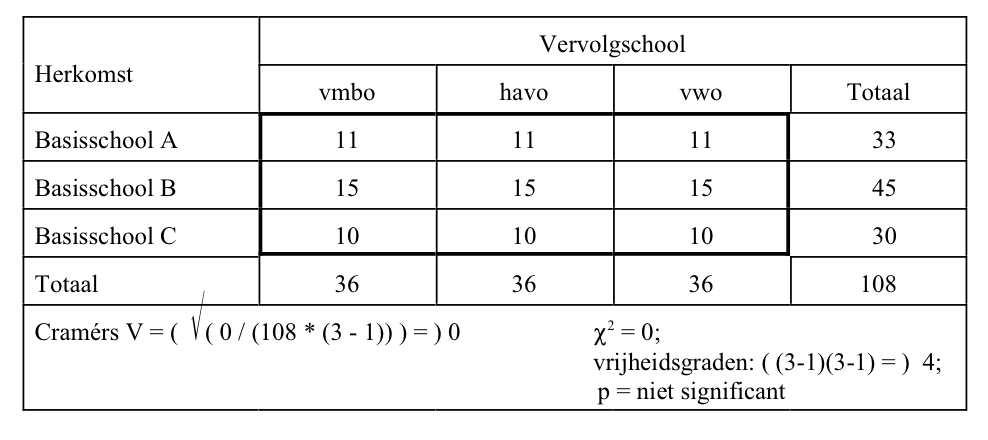
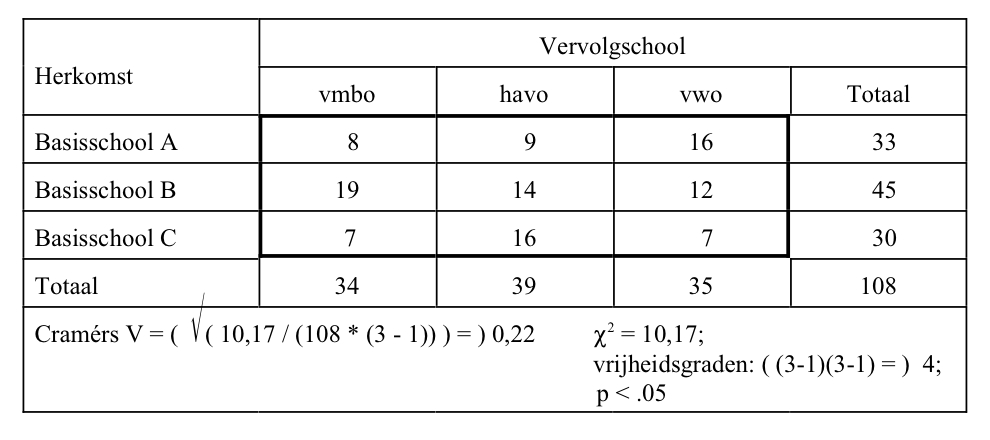
Het mooie hiervan is dat de interpretatie van Cramérs V in grote lijnen overeenkomt met de andere maten voor samenhang op ordinaal en interval niveau. In de illustraties hieronder staan een aantal voorbeelden.  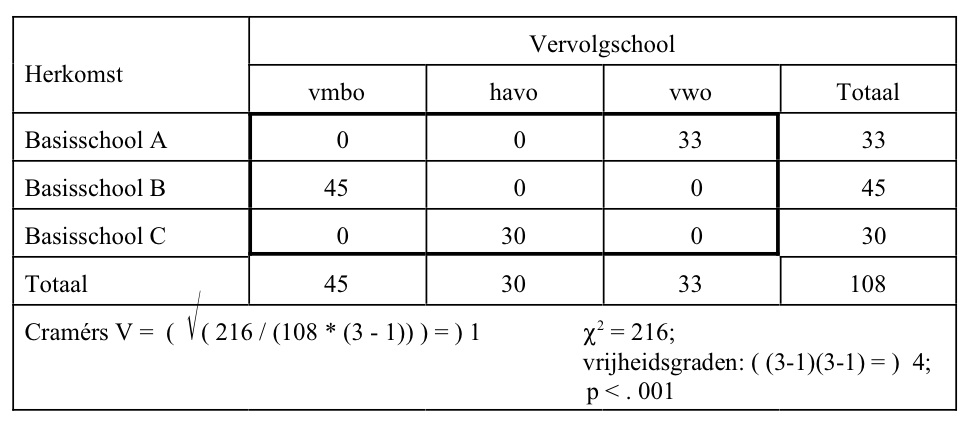In bovenstaande tabellen is er een oplopende Cramérs V van 0 (volledig gelijkelijk verdeeld over de cellen) tot 1 (bij iedere kolom hoort 1 rij waarin waarden staan). Of Cramérs V van 0 afwijkt wordt getoetst met behulp van de Chikwadraattoets. Op nominaal niveau geldt: het toetsen of er een samenhang is, is hetzelfde als het toetsen of er een verschil is.

Cramer V wordt ook besproken in onze Cursus Statistiek en in de video van de Cursus SPSS leggen we uit hoe je die maat in SPSS tevoorschijn tovert.

© Foeke van der Zee (2017). hulpbijonderzoek.nl/online-woordenboek

- specialist in Onderzoek en Statistiek

- auteur van boeken over onderzoek

Aan Cramers V gerelateerde trefwoorden:

- chikwadraattoets

- phi-coëfficiënt

Met onze cursussen wordt onderzoek zo veel makkelijker en leuker. En het scheelt je uren tijd. Beter kun je het niet krijgen.

Cursus methodologie
Met de informatie in deze cursus doe je altijd perfect onderzoek. Je krijgt info over het hele onderzoeksproces; van A tot Z; van onderzoeksvraag tot onderzoeksverslag.
Meer informatie >>>


Cursus Statistiek 
Als je twee getallen kunt vergelijken, kun je ook statistiek leren. Als je onze video's bekijkt, wordt statistiek een makkie. Het is een cursus toegepaste statistiek, dus uiterst bruikbaar voor je thesis.
Meer informatie >>>

Cursus SPSS 
In online video's leggen we je uit op welke knoppen je moet drukken om de juiste uitvoer te krijgen.  We leggen je ook uit waar je in de uitvoer op moet letten om het analyseresultaat te interpreteren.
Meer informatie >>>