Hulp bij onderzoek

Kendalls tau is een maat voor samenhang voor variabelen op ordinaal niveau. Deze maat is vergelijkbaar met de Spearman rangcorrelatie, maar is een beetje 'conservatiever'.

Een voorbeeld voor het toepassen van Kendalls tau

Bijvoorbeeld. Als twee docenten verschillende leermethoden moeten beoordelen, kunnen ze dat aangeven met de beste, de een na beste etc. Stel dat tien studieboeken worden beoordeeld door twee docenten en dat elke docent moet aangeven welk boek hij het meest geschikt acht, welk als tweede etc. Je kan je nu afvragen in welke mate de docenten het met elkaar eens zijn. De maat om die mate van samenhang te berekenen is Kendall's tau.

De formule voor Kendalls tau

Kendalls tau wordt berekend met behulp van de volgende formule: 

De waarde die uit deze formule komt, ligt altijd tussen de -1 en +1. Interpretatie van de uitkomst is dezelfde als bij de productmoment correlatie. De waarde van 0 betekent geen verband en hoe dichter bij 1 of -1 des te meer is er sprake van een één op één relatie.

Een rekenvoorbeeld voor Kendalls tau

De procedure verloopt als volgt. Van de eerste docent zet je de oordelen op de logische rangvolgorde. Het oordeel van de tweede docent zet je erachter. Dit zal - tenzij beide docenten het volstrekt met elkaar eens zijn - niet dezelfde rangvolgorde opleveren. Vervolgens let je uitsluitend en alleen op de tweede beoordelaar. Bij iedere rangscore tel je het aantal hogere volgordenummers eronder. Dit is het aantal 'agree'. Ook tel je het aantal hogere oordelen erboven. Dit is het aantal disagree'. Vervolgens tel je elke kolom op om een totaalscore voor agree en disagree te vinden. Ter controle kun je vaststellen of het totaal aan agree en het totaal aan disagree overeenkomt met (n * (n - 1) ) / 2.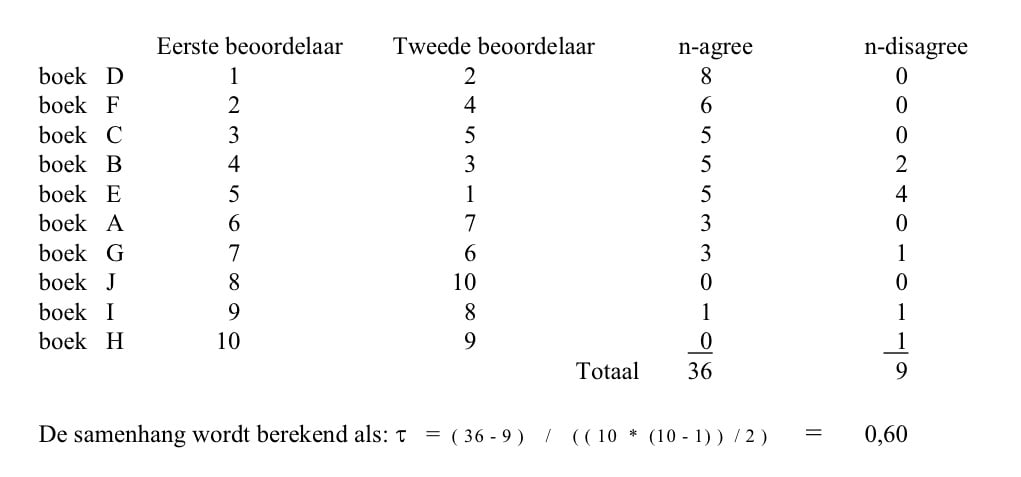 

Alternatieve formules voor Kendalls tau

Omdat n_(agree) en n_(disagree) elkaars complement zijn, kan men ook een van beide volgende formules gebruiken: 

Er gelden twee voorwaarden: 1) n > 10 en 2) er zijn geen knopen. Zijn die er wel, dan wordt het wat lastiger om Kendalls tau met de hand te bereken. Hoe dat moet leggen we uit in de video´s over statistiek. Het berekenen van Kendalls tau is makkelijk te doen in SPSS. Dat leggen we je graag aan je uit in de video´s over SPSS.

© Foeke van der Zee (versie 2023). hulpbijonderzoek.nl/online-woordenboek

- specialist in Onderzoek en Statistiek
- auteur van boeken over onderzoeksmethodologie
- oprichter van en coach bij Hulp bij Onderzoek

Aan Kendalls tau gerelateerde trefwoorden:

- correlatie
- Spearman rangcorrelatie

Terug naar de begrippenlijst