Hulp bij onderzoek

Correlatie is de (rekenkundige) maat voor samenhang. De maat ligt altijd tussen -1 en +1. Bij -1 of +1 is er een perfecte relatie. Is de waarde 0 dan is er helemaal geen relatie tussen de variabelen.

Hoe bereken je de correlatiecoëfficiënt?

De meest bekende maat voor samenhang is de Pearson productmoment correlatiecoëfficiënt (r). Deze kan alleen worden berekend als beide variabelen op interval of ratio niveau zijn gemeten. Er zijn twee formules om de correlatiecoëfficiënt te berekenen, maar de gemakkelijkste is deze: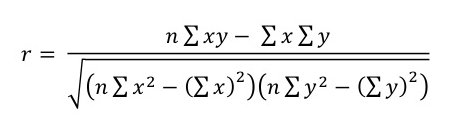 

De uitkomst uit deze formule ligt altijd tussen -1 en +1. Heb je een andere uitkomst, dan heb je een rekenfout gemaakt.

Interpretatie van de correlatiecoëfficiënt

De interpretatie van de uitkomst is als volgt. Ligt de rekenkundige uitkomst tussen 0 en 1 dan spreekt men van een positieve samenhang: als de score op de ene variabele omhoog gaat, gaat de score op de andere variabele ook omhoog. Is de waarde 1 dan is er een perfecte samenhang tussen beide variabelen: de gegevens liggen op één rechte lijn.

Bij een negatieve uitkomst is er sprake van een negatieve samenhang: als de score op de ene variabele omhoog gaat, gaat de score op de andere variabele naar beneden.

Is de uitkomst 0, dan is er geen samenhang. Je kun dan niet aangeven of de toename in de ene variabele overeenkomt met een toe- of afname in de andere variabele. Dit is ook uit te beelden in een puntenwolk:

Correlatie en het niveau van de variabelen

Zijn beide variabelen op ordinaal niveau gemeten dan kan je beter de Spearman rangcorrelatie of Kendalls Tau berekenen. De interpretatie van de uitkomst is hetzelfde als hierboven voor de productmoment correlatie. Zijn beide variabelen op nominaal niveau gemeten dan berekent men bij voorkeur Cramers V maar als beide variabelen een dichotomie zijn, dan berekent men de phi-coëfficiënt.

Voor variabelen op nominaal niveau spreekt men ook wel van een maat voor associatie in plaats van correlatie. Deze waarde ligt altijd tussen 0 en 1, maar is op dezelfde manier te interpreteren als de productmoment correlatie.

Correlatie en multipele correlatie

Bovenstaande maten zijn alleen bruikbaar voor een combinatie van twee variabelen. Wil men een samenhang berekenen van één variabele met twee of meer variabelen dan kan men de multipele correlatiecoëfficiënt (R²) berekenen. Een ander naam daarvoor is canonische correlatie. De multipele correlatie kan eigenlijk alleen berekend worden tussen variabelen op interval niveau. Het wordt echter ook veelvuldig gebruikt voor het berekenen van een samenhang van één continue variabele en één (of meer) continue variabelen in combinatie met dummy-variabelen.

Correlatie is het hart van de statistiek

Correlatierekening wordt door velen als de basis van statistiek gezien. Het is in ieder geval de grondslag voor regressieanalyse.

© Foeke van der Zee (versie 2023). hulpbijonderzoek.nl/online-woordenboek

- specialist in Onderzoek en Statistiek
- auteur van boeken over onderzoeksmethodologie
- oprichter van en coach bij Hulp bij Onderzoek

Aan correlatie gerelateerde termen:

Spearman's rangcorrelatie
Kendalls tau
Cramers V
phi-coëfficiënt
Multipele correlatie
Regressieanalyse
Multipele regressie

Terug naar de begrippenlijst