Standaarddeviatie

Het is belangrijk om te weten of de getallen in een reeks dicht rondom het gemiddelde liggen, of dat ze meer verspreid zijn over de gehele range. De indicator daarvoor is de standaarddeviatie. Dit is de statistische term. In alledaags taalgebruik noemt men dit de spreiding of ook wel de standaardafwijking.

Hoe bereken je de standaarddeviatie?

De standaarddeviatie is een rekenkundige maat voor de spreiding van de getallen rondom het gemiddelde. Als er weinig spreiding is dan liggen de getallen allemaal dicht bij elkaar op een hoopje. Het nadeel van een variabele met weinig spreiding is dat het niet veel varieert en dat je ook weinig statistisch significante verschillen of verbanden zult vinden. De formule voor het berekenen van de standaarddeviatie is de volgende: De standaarddeviatie is een rekenkundige maat voor de spreiding van de getallen rondom het gemiddelde.

Interpreteren van de standaarddeviatie

Als er helemaal geen variatie in de getallenreeks is dan is de uitkomst 0 (nul). Alle getallen komen dan overeen met het gemiddelde. Verder kan de standaarddeviatie in theorie oplopen tot plus oneindig. In de praktijk is de grootte van de standaarddeviatie afhankelijk van de range (het laagste minus het hoogste getal). Is de range groot dan heeft men ook een grote standaarddeviatie.

Met de standaarddeviatie kun je uitbijters opsporen

De standaarddeviatie kan gebruikt worden als indicator voor het normaal verdeeld zijn van de variabele. Als vuistregel geldt dat er in het interval dat bepaald wordt door het gemiddelde plus één maal de standaarddeviatie (de bovengrens) en het gemiddelde min één maal de standaarddeviatie (de ondergrens), ongeveer 69% van alle waarden voor moet komen. Bij plus of min twee maal de standaarddeviatie ligt ongeveer 95%, en bij plus of min drie maal de standaarddeviatie ligt 99% (zie illustratie hieronder). Is dit niet het geval dan heeft men een andere verdeling.

Het is belangrijk om te weten of de getallen in een reeks dicht rondom het gemiddelde liggen, of dat ze meer verspreid zijn over de gehele range. De indicator daarvoor is de standaarddeviatie.

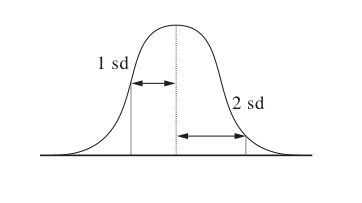
Met behulp van de standaarddeviatie zijn ook uitbijters (dat zijn gegevens die flink afwijken van de rest) aan te wijzen. Je kan ze verwijderen door te stellen dat uitbijters niet boven 4 of 5 maal de standaarddeviatie plus of min het gemiddelde mogen uitkomen. Als een uitbijter wordt weggelaten, moet daarna natuurlijk wel opnieuw het gemiddelde en de spreiding worden berekend.