Hulp bij onderzoek

Scheefheid (skewness) is de maat die aangeeft of een verdeling links- of rechtsscheef verdeeld is in vergelijking met de normaal-verdeling.

Als je gegevens verzamelt over een kenmerk, dan veronderstel je soms dat deze gegevens normaalverdeeld zijn. Kenmerkend voor een normaalverdeling is dat het gemiddelde precies in het midden ligt en dat de verdeling aan beide kanten gelijkmatig afneemt. Dat is natuurlijk niet altijd het geval.

Manieren om scheefheid vast te stellen

De meest simpelste manier om na te gaan of een kenmerk normaalverdeeld is, is het uitprinten van de frequenties en uit de frequentieverdeling nagaan of deze op een normaalverdeling lijkt. Dit kan worden ondersteund door de verdeling te visualiseren: presenteer de gegevens in een histogram of een staafdiagram.

Andere indicatoren voor het normaalverdeeld zijn van een variabele is dat het gemiddelde, de modus en de mediaan allemaal gelijk zijn. Blijkt dit niet het geval te zijn, dan moet men concluderen dat de verdeling niet normaalverdeeld is.

Het zal zelden voorkomen dat de modus, de mediaan en het gemiddelde precies gelijk zijn en een visuele beoordeling is natuurlijk ook niet erg nauwkeurig. Het kan beter door de scheefheid (in het Engels: skewness) en de kurtosis te berekenen en te interpreteren.

Twee vormen van scheefheid

Bij scheefheid wordt een onderscheid gemaakt naar links-scheef en rechts-scheef. Bij links-scheef ligt de staart links. De waarnemingen aan de linkerkant liggen verder weg van het midden dan aan de rechterkant. Men kan zich dit visueel voorstellen als een glijbaan, waarbij je aan de linkerkant naar beneden glijdt. Of als een dier: de staart ligt links. Bij rechts-scheef is het juist andersom: de waarnemingen aan de rechterkant van het midden liggen verder weg van het midden (zie illustratie).

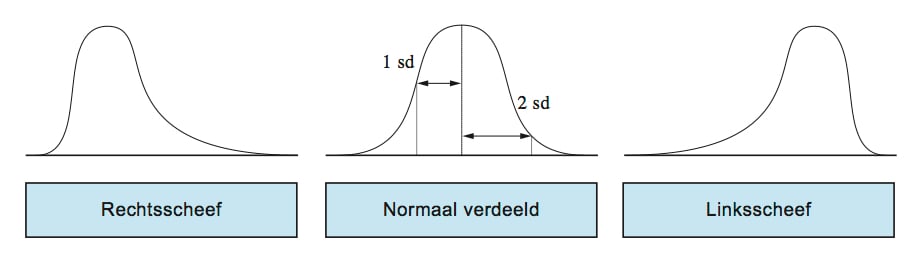
Het berekenen van scheefheid

Rekentechnisch is het allemaal wat moeilijker. De formule voor de scheefheid is de volgende: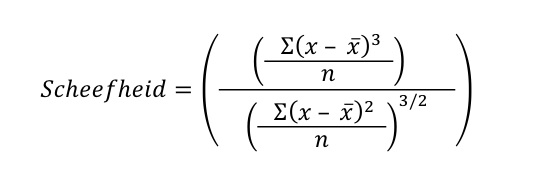 

Een links-scheve verdeling heeft een negatieve waarde, een rechts-scheve verdeling heeft een positieve waarde. Ligt het gemiddelde precies in het midden dan is de waarde van de scheefheid 0. Helemaal exact nul zal de waarde nooit zijn. Als vuistregel geldt dat waarden tussen -0,5 en +o,5 indicatief zijn voor een goede normale verdeling. Waarden tussen -1 en +1 duiden op een redelijk goede normaal verdeling en waarden kleiner dan -1 of groter dan +1 zijn indicatief voor niet normale verdelingen.

© Foeke van der Zee (versie 2023). hulpbijonderzoek.nl/online-woordenboek

- specialist in Onderzoek en Statistiek
- auteur van boeken over onderzoeksmethodologie
- oprichter van en coach bij Hulp bij Onderzoek

Aan Scheefheid gerelateerde relevante trefwoorden:

- kurtosis
- gemiddelde
- mediaan
- modus
- range
- standaarddeviatie (spreiding, variantie)
- uitbijters

Terug naar de begrippenlijst